
FFT is an algorithm used to compute the Discrete Fourier Transform (DFT) and its inverse efficiently. The DFT converts a sequence of values into components of different frequencies, which is useful in many fields such as signal processing, image analysis, and data compression.
Mathematical Formulation:
Given a sequence x[n] of length n, the DFT X[k] is defined by:
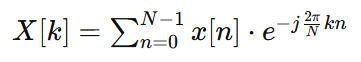
where:
X[k] is the k-th frequency component.
x[n] is the n-th time-domain sample.
The FFT algorithm reduces the computational complexity of calculating the DFT from O(N2) to O(NlogN). This is achieved by decomposing the DFT into smaller DFTs recursively, exploiting symmetries and periodicities in the Fourier coefficients.
IFFT is used to convert data from the frequency domain back into the time domain. It is essentially the reverse operation of the FFT.
Mathematical Formulation:
Given the frequency domain sequence X[k], the IFFT x[n] is defined by:
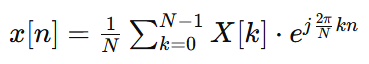
where:
x[n] is the n-th time-domain sample.
X[k] is the k-th frequency component.
In practice, both FFT and IFFT are implemented efficiently in numerical libraries and software packages, making them essential tools for many digital signal processing tasks.
Numerical Recipes: The Art of Scientific Computing by William H. Press et al.
The Fast Fourier Transform and its Applications by E. Oran Brigham.
Understanding Digital Signal Processing by Richard G. Lyons.
Fourier Analysis and Its Applications by Gerald B. Folland.
These resources provide a range of perspectives on FFT and IFFT, from practical implementation to theoretical foundations.
The following explains the inputs required for generating time-series data using various mathematical functions like cosine, sine, tangent, cotangent, and power functions. These inputs allow flexibility in defining the function and controlling the sampling rate and duration.
Description: Specifies the type of mathematical function to generate the time series.
Accepted Values:
cos: Cosine function : \(a \cdot \cos(2 \cdot \pi \cdot b \cdot t + c)\)sin: Sine function : \(a \cdot \sin(2 \cdot \pi \cdot b \cdot t + c)\)tan: Tangent function : \(a \cdot \tan(2 \cdot \pi \cdot b \cdot t + c)\)cot: Cotangent function : \(\frac{a}{\tan(2 \cdot \pi \cdot b \cdot t + c)}\)pow: Power function : \(a \cdot t^b + c\)a)Description: Amplitude or scaling factor for the function.
Effect: Scales the output of the function by this value.
Example:
cos: \(a = 2\), the function becomes \(2 \cdot \cos(…)\).pow: \(a = 3\), the function becomes \(3 \cdot t^b + c\).b)Description: Frequency parameter (in Hz) for trigonometric functions (cos, sin, tan, and cot). For pow, it represents the exponent.
Effect:
pow, it determines the exponent \(t^b\).Example:
cos: \(b = 2\), the function oscillates twice per second.pow: \(b = 2\), the function becomes \(t^2\).c)Description: Phase offset for trigonometric functions or a constant for the power function.
Effect:
pow, adds \(c\) to the computed value \(a \cdot t^b\).Example:
sin: \(c = \frac{\pi}{2}\), the waveform shifts by \(\frac{\pi}{2}\) radians.pow: \(c = 5\), the function becomes \(a \cdot t^b + 5\).Description: The number of samples taken per second from the continuous function.
Effect: Determines the resolution of the generated time series. Higher values produce more precise data.
Constraints: Must be greater than 0.
Example:
Description: The total duration (in seconds) for which the time series is generated.
Effect: Controls the length of the time series.
Constraints: Must be greater than 0.
Example:
This website uses cookies to provide you with the best browsing experience.